
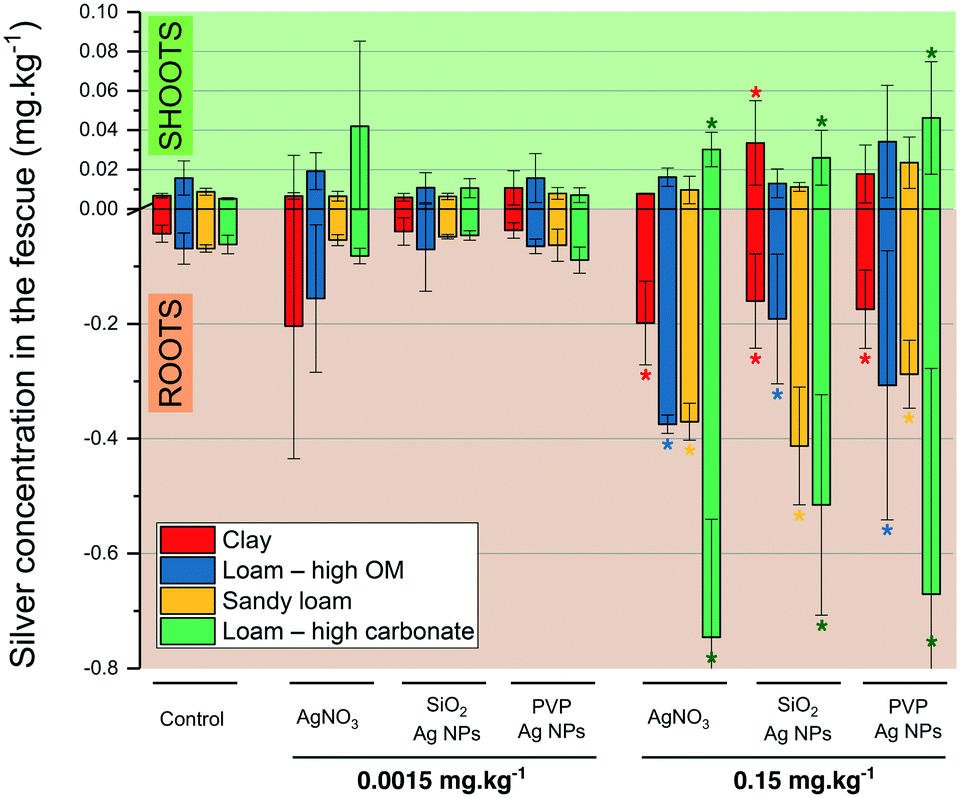
Standard Classical one-way ANOVA can be viewed as an extension to the classical "2-sample T-test" to an "n-sample T-test". However, unless you have an enormous amount of data, near-normality of the residuals is essential for p-values computed from the F-distribution to be meaningful. The point is that what you're looking it is not relevant.ĪNOVA residuals don't have to be anywhere close to normal in order to fit the model. You could, by luck, make the correct determination: that is, by looking at the raw data you will seeing a mixture of distributions and this can look normal (or not). If there are significant and important effects in the data (as in this example), then you might be making a "grave" mistake. Note also that the p-values are computed from F (or t) statistics and those depend on residuals, not on the original values. The distribution of the residuals matters, because those reflect the errors, which are the random part of the model. The errors might (or might not) be normally distributed, but obviously this is a completely different distribution. Then all residuals range from -30 to +30, and so the errors will be expected to have a comparable distribution. Suppose further the average yields are 100 and 500, respectively. The distribution of results is strongly non-normal: it's clustered at two locations related to the fertilizer application. In two plots with fertilizer the yield ranged from 470 to 530. In plots without fertilizer the yield ranged from 70 to 130. Suppose you measured yield from a crop with and without a fertilizer application. No, normality (of the responses) and normal distribution of errors are not the same. The assumptions, therefore, are about the errors, not the residuals. With sufficiently large amounts of data and a good fitting procedure, the distributions of the residuals will approximately look like the residuals were drawn randomly from the error distribution (and will therefore give you good information about the properties of that distribution).
(The advice doesn't really change for random-effects models, it just gets a little more complicated.)įirst let us distinguish the "residuals" from the "errors:" the former are the differences between the responses and their predicted values, while the latter are random variables in the model.
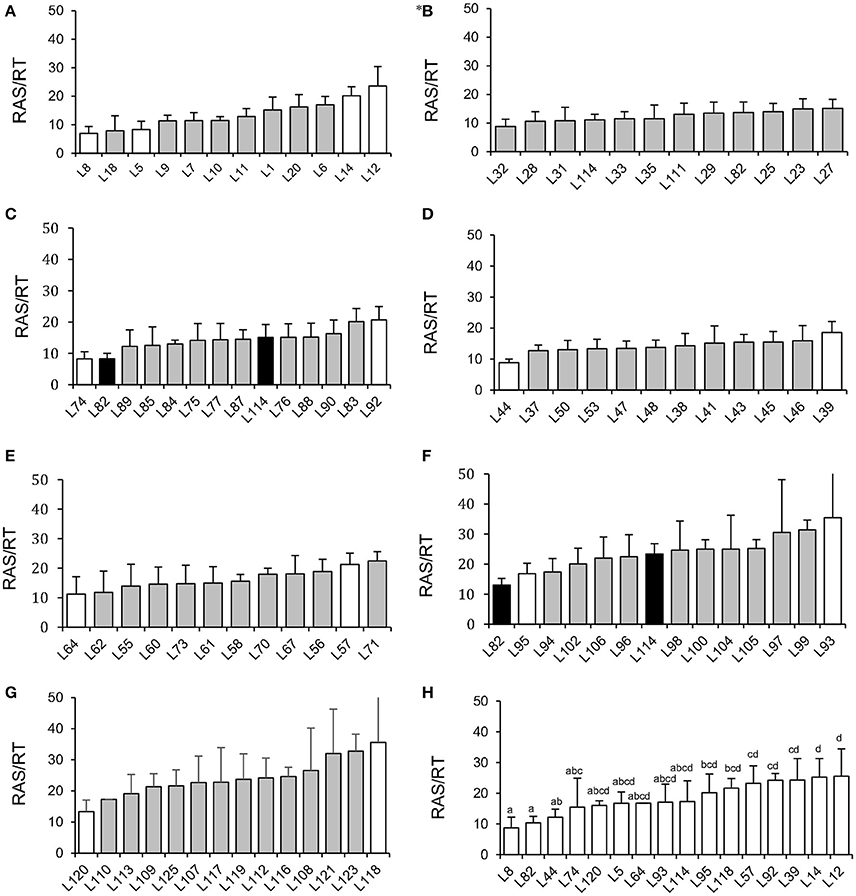
The results show that in this particular study area, Level 1 models, even BDF, are quite accurate, but the above modelling strategy maximises the extracted information from the local data and BMA reveals that the higher uncertainties occur at areas with higher vulnerability whereas lower uncertainties are observed at areas with lower vulnerabilities.Let's assume this is a fixed effects model. The model performance is tested by using the nitrate-N concentrations measured for the aquifer. BMA is naturally an Inclusive Multiple Modelling (IMM) strategy at two levels at Level 1 multiple models are constructed and the paper constructs three AI (Artificial Intelligence) models, which comprise ANN (Artificial Neural Network), GEP (Gene Expression Programming), and SVM (Support Vector Machines) but their outputs are fed to the next level model at Level 2, BMA combines ANN, GEP and SVM (the Level 1 models) to quantify their inherent uncertainty in terms of within and in-between model errors. Bayesian Model Averaging (BMA) is used to study inherent uncertainties using the Basic DRASTIC Framework (BDF) for assessing the groundwater vulnerability in a study area related to Lake Urmia.


 0 kommentar(er)
0 kommentar(er)
